dalao室友突然提出一个他看到的有趣的问题: 在一个圆内均匀随机取4个点,落在同一个半圆内的概率(半圆圆心与原来的圆相同)。
首先因为均匀随机点也是均匀随机圆周角,所以实际上是问: 在一个圆周上均匀随机取4个点,在同一个半圆弧上的概率。
一般化地,我考虑随机取n个点的情况,本文将讨论n≤4并推广到任意n。本文将以"大学数学"和"小学数学"两条思路进行。
n≤2
答案是1。
n=3
大学数学
暴力积分: 假设有两个点已经确定夹角为θ,那么第三个点可以取的角度弧度制范围是(以第一个点为基准零点): [θ−π,π]。于是答案就是:
π1∫0π2ππ−(θ−π)dθ=π1(π−2π1∫0πθdθ)=43
小学数学
三个点都在一个半圆周上等价于三个点连成的三角形在圆心的一侧,即不包含圆心。例如:
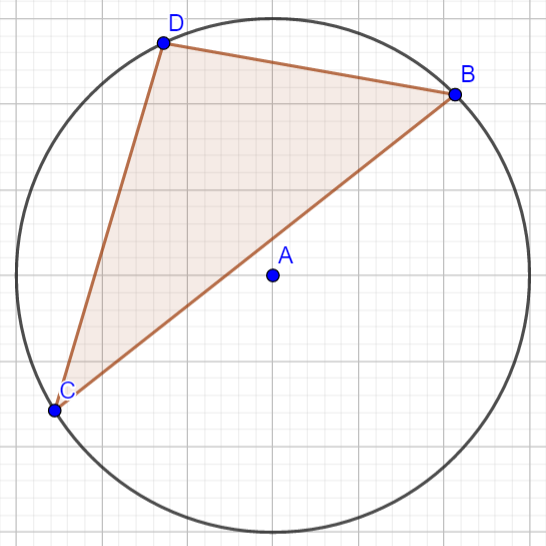
那么怎么求这个概率呢?考虑下图作射线BA和CA:
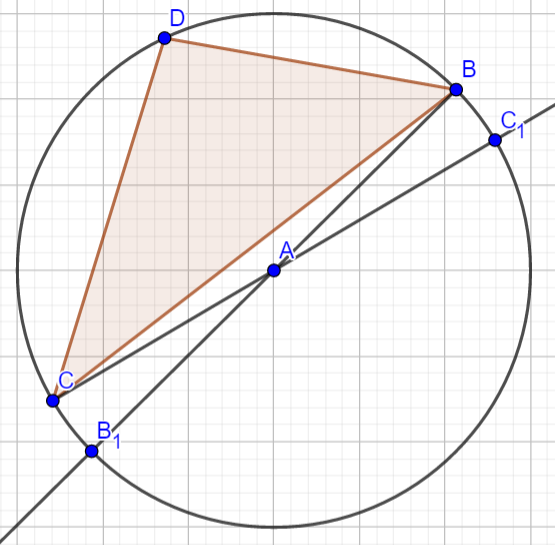
这时候枚举B,C和枚举BA,BC再确定点B和C是等价的。于是枚举BA,BC即可。
这时候能得到这样一个图形的有四种可能的三角形ΔDBC,ΔDBC1,ΔDB1C,ΔDB1C1。只有一种包含圆心,即ΔDB1C1。不难发现这总是成立的。
又因为我们之前构造了一种对应关系,所以分布是均匀的: 每四个三角形中有一个不满足条件,因此答案为43。
概括来说,过圆心做两条直径,每条直径分别选一个端点可以得到四种不同的方案。枚举不同的直径可以唯一且不遗漏得到一个圆周上取点的方案。这样的得到的每组四种方案中都有且仅有一种不合法。
答案是43。
n=4
大学数学
还是暴力积分。n=3的问题通过积分转化为一个面积问题,这里n=4就转化为体积问题。
这回要多分类讨论一样,就是一个二元函数: θ1,θ2分别表示第一个点和第二个点的夹角,第一个点和第三个点的夹角,p(θ1,θ2)表示第四个点的取值合法概率。得到一个三维立体图。
首先底面是θ1和θ2本身有限制:
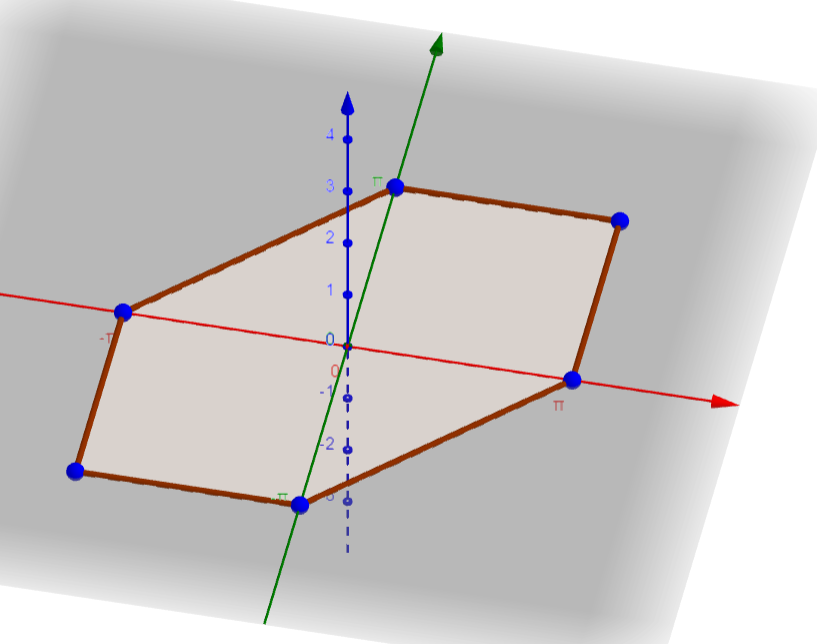
然后分类讨论第四个点的概率,得到的图形是底面六边形形成一个高为21的六棱柱,然后顶部每个点再连向(0,0,1):
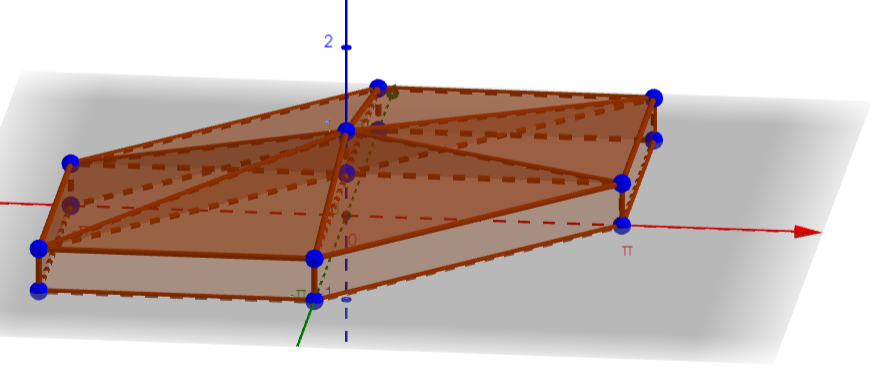
这个多面体体积为21×(1+31)×3π2=2π2,除以总事件空间体积(代表方案数)2π×2π×1=4π2,就得到21。
因此答案是21。
小学数学
似乎之前的方法非常巧妙,对于n=4就不适用了。
不过还是考虑通过构造"新方案"来解决问题。
这个问题麻烦在于点之间的相对关系不确定,如果关系确定就好办了: 对于一种选择四个点的方案,强制将随机一个点作为第一个点,且卡在顺时针半圆起始边界上。例如:
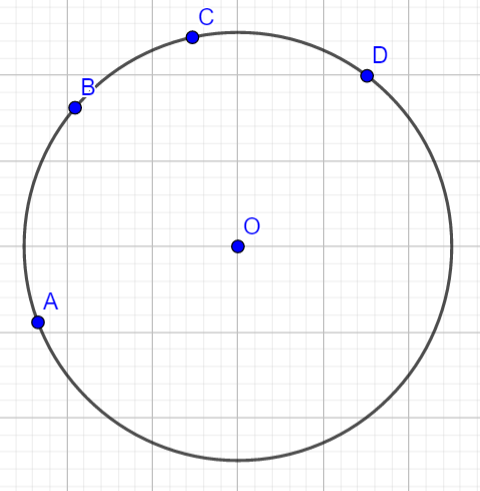
如果选择A点作为起点,就只判断四个点是否在如下半圆内:
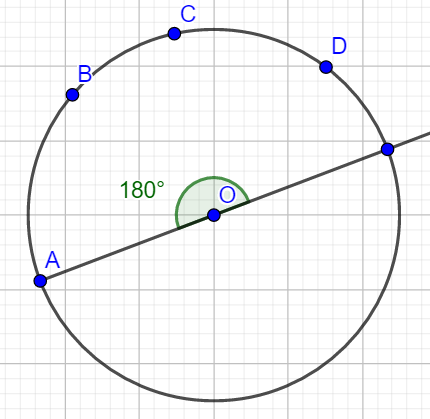
这样我们构建了一个"新方案": 原来每个方案取四个点中的任意一个作为起点可以构造四个"新方案"。
"新方案"满足四个点在这样一个已经固定好的半圆内的概率很好算: 除了第一个点用来确定半圆外剩下三个点都是随机取的,有21的概率在半圆内,因此有81的方案满足,87的方案不满足。
接下来鸡兔同笼的骚操作就来了:
而对于原来的只有选择四个点的方案: 如果这个方案是不合法的(不存在一个半圆使得四个点在同一个半圆内),那么显然四种起点的选择都不满足条件;如果这个方案是合法的,那么只有一种起点的选择方案满足,其余总会出现在起点逆时针方向有点的情况。
因此每个合法方案对满足条件的"新方案"贡献为1,对不满足条件的新方案贡献为3;每个不合法方案对不满足条件的新方案贡献为4。
那么设合法方案比例为p,"新方案"比例系数为Ω。就有:
{4(1−p)+3p=87Ωp=81Ω
就解得p=21。这样就好像鸡兔同笼问题,假设已知总动物数,然后知道物种A(合法方案)有1只眼3条腿,物种B(不合法方案)没有眼睛有4条腿,然后知道总的眼睛数和腿数之比,就求出物种A和B之比。
n∈N+
大学数学
高维体积?
似乎并不好做了。
小学数学
n=4的情况完全可以无压力推广:
任选一个点作为起点,原先一个方案可以构造出n个新方案。一个合法方案会构造出1个满足条件,n−1个不满足条件的新方案;一个不合法方案会构造出n个不满足条件的新方案。
总的新方案合法比例是n−1个点任取在一个固定半圆内的概率2n−11。
因此,就得到方程组:
{n(1−p)+(n−1)p=2n−12n−1−1Ωp=2n−11Ω
解得通解p=2n−1n。其中要求n≥1。当n=1时p=1;当n=2时p=2;当n=3时p=43;当n=4时p=21。符合情况。
因此这个问题的答案就是2n−1n。
扫描二维码即可在手机上查看这篇文章,或者转发二维码来分享这篇文章:








