给定一个收敛数列，近似估计这个数列的收敛值至所要求的的精度。例如:

$1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - ... = \frac{\pi}{4}$

假设我们还不知道$\pi$是多少，要近似到$10^{-9}$精度则需要计算接近$10^{9}$数量级这么多项，这是不能接受的。

有什么办法可以快速求这个收敛值的近似值呢？

Shanks变换(Shanks Transformation)

记$s_n(A)$表示序列$A$的前$n$项和。对于一个序列$A$，现在想要快速求出其收敛值$S = s_{+\infty}(A) = \sum A_i$。

构造序列$B$，使得$s_n(B) = S + \alpha q^n$。其中$0 \lt \vert q \vert \lt 1$。我们可以通过联立方程组来获得这样一个解法:

$\begin{cases} s_{n+1}(B) = S + \alpha q^{n+1} \\ s_n(B) = S + \alpha q^n \\ s_{n-1}(B) = S + \alpha q^{n-1} \\ \end{cases} \\ \Rightarrow (s_{n-1}(B)-S)(s_{n+1}(B)-S)= (s_n(B)-S)^2$

化简就得到与$\alpha,q$无关的式子:

$S = \frac{s_n^2(B)-s_{n-1}(B)s_{n+1}(B)}{2s_n(B)-s_{n-1}(B)-s_{n+1}(B)}$

注意目前为止这个等式对于任何$n$都严格成立(在极限意义下)而非一个近似估计。

但是毕竟我们不知道序列$B$的表达式，不能直接拿来计算(如果能的话不就做完了)。于是接下来，Shanks变换假设$s_n(B)$可以近似地等于$s_n(A)$。

$\hat S_{1,n} = \frac{s_n^2(A)-s_{n-1}(A)s_{n+1}(A)}{2s_n(A)-s_{n-1}(A)-s_{n+1}(A)}$

只要代入$s_{n-1}(A),s_n(A)$和$s_{n+1}(A)$的函数值，我们就得到了一个关于$S$的估计值$\hat S_{1,n}$。特别地，如果分母是$0$就认为$\hat S_{1,n} = s_n(A)$。

显然在$n$越大的时候由于$s_n(A)$和$s_n(B)$都越来越接近最后的答案$S$，$S$就越接近$\hat S_{1,n}$，估计越准确。这里构造$\alpha q^n$作为一个附加项，就是因为$\alpha q^n$衰减得很快，可以让序列$B$在尽可能小的$n$就与序列$A$接近，使得将$s_n(B)$替换为$s_n(A)$的误差较小，而且最终$\lim_{n \rightarrow +\infty}s_{n}(B) = S$。

事实上，Shanks变换的这个近似假设往往是比较准确的。如果我们接受Shanks变换比普通迭代更有效的事实，那么就可以嵌套Shanks:

$\hat S_{i+1,n} = \frac{\hat S_{i,n}^2-\hat S_{i,n-1}\hat S_{i,n+1}}{2\hat S_{i,n}-\hat S_{i,n-1}-\hat S_{i,n+1}}$

代码实测一下:

#include <bits/stdc++.h>
using namespace std;
#define EPS 1e-15
#define MAXN 100000
#define db long double
#define rint register int
inline int rf(){int r;int s=0,c;for(;!isdigit(c=getchar());s=c);for(r=c^48;isdigit(c=getchar());(r*=10)+=c^48);return s^45?r:-r;}
db A[16][MAXN+5], _; int n, K; inline db Shanks(db a, db b, db c){return _=2*b-a-c,fabs(_)>EPS?(b*b-a*c)/_:b;}
int main(){
    n = rf(); K = rf(); A[K][0] = 1; printf("pi = %.10Lf\n",(db)3.1415926535897932384626433832795);
    for(rint i = 1; i <= n+K; A[K][i] = A[K][i-1]+(db)(i&1?-1.:1.)/(i<<1|1), i++);
    for(rint j = K-1, i; ~j; j--) for(i = 1; i <= n+j; i++)
        A[j][i] = Shanks(A[j+1][i-1],A[j+1][i],A[j+1][i+1]);
    printf("         "); for(rint j = 0; j <= K; printf("Shanks %2d:   ",j), j++); puts("");
    for(rint i = 1, j; i <= n; i++)
        for(printf("n = %3d: ",i), j = K; ~j; printf("%.10Lf%c",4*A[j][i],"\n "[!!j]), j--);
    return 0;
}

下面是实测结果:

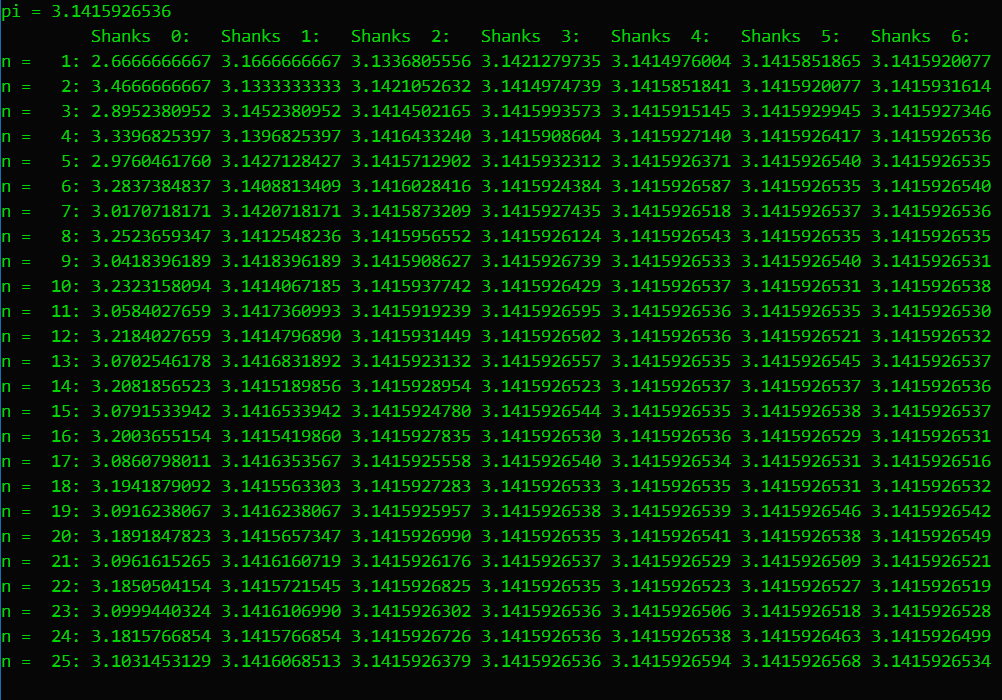
可以发现精度是非常高的，$\hat S_{6,25}$已经达到了精度要求，完全不需要计算$10^9$项。

Richardson外推法(Richardson Extrapolation)

Richardson外推法是另外一种加速级数求和的方式。Shanks变换一般对于交错数列($A_i$每项一正一负)效果更好，而Richardson外推法对于单调数列效果更好。

Richardson外推法思路和Shanks变换几乎完全一样。不过，Shanks变换构造$s_n(B) = S + \alpha q^n$，而Richardson外推法则构造:

$s_n(B) = S + \sum_{i=1}^{+\infty}\frac{A_i}{n^i}$

先只计算第一项，联立方程组:

$\begin{cases} s_{n+1}(B) = S + \frac{A_1}{n+1} \\ s_n(B) = S + \frac{A_1}{n} \\ \end{cases} \\$

用$n+1$倍的①式减去$n$倍的②式，得到的结果:

$S = (n+1)s_{n+1}(B) - ns_n(B)$

同样地，目前为止严格精确。因为同样满足$\lim_{n \rightarrow +\infty}s_n(B) = S$，所以同样地，Richardson外推法假设$s_n(B)$可以近似地等于$s_n(A)$。

$\hat R_{1,n} = (n+1)s_{n+1}(A) - ns_n(A)$

这称为$1$阶Richardson外推法。

与Shanks变换不同，高阶Richardson外推法不是通过迭代这一过程而是通过增加展开的项数。在之前的Richardson外推法假设公式中，我们计算两项:

$\begin{cases} s_{n+2}(B) = S + \frac{A_1}{n+2} + \frac{A_2}{(n+2)^2} \\ s_{n+1}(B) = S + \frac{A_1}{n+1} + \frac{A_2}{(n+1)^2} \\ s_n(B) = S + \frac{A_1}{n} + \frac{A_2}{n^2} \\ \end{cases} \\$

计算$(n+2)^2$①$-2(n+1)^2$②$+n^2$③，化简后近似可以得到$2$阶Richardson:

$\hat R_{2,n} = \frac{(n+2)^2s_{n+2}(A) - 2(n+1)^2s_{n+1}(A) + n^2s_n(A)}{2}$

然后类似地计算$3$阶Richardson:

$\hat R_{3,n} = \frac{(n+3)^3s_{n+3}(A)-3(n+2)^3s_{n+2}(A)+3(n+1)^3s_{n+1}(A)-n^3s_n(A)}{6}$

就可以发现规律，对于任意的$k$展开$k$阶以后模仿上述步骤，就可以得到$k$阶Richardson公式:

$\hat R_{k,n} = \frac{1}{k!} \sum_{i=0}^k (-1)^{k-i}C_k^i(n+i)^ks_{n+i}(A)$

由于Richardson不擅长处理交错数列，我们改用$\zeta(2)$来检验其有效性:

$1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + ... = \frac{\pi^2}{6}$

代码实现:

#include <bits/stdc++.h>
using namespace std;
#define MAXN 100000
#define db long double
#define PI 3.1415926535897932384626433832795
#define rint register int
inline int rf(){int r;int s=0,c;for(;!isdigit(c=getchar());s=c);for(r=c^48;isdigit(c=getchar());(r*=10)+=c^48);return s^45?r:-r;}
db A[MAXN+5], _; int n, K; long long C[16][16], fac[16];
inline db Richardson(int k, int n){_ = 0; for(rint j = 0; j <= k; _ += ((k-j)&1?-1:1)*C[k][j]*powl(n+j,k)*A[n+j], j++); return _/fac[k];}
int main(){
    for(rint i = C[0][0] = 1, j; i <= 15; i++) for(j = C[i][0] = 1; j <= 15; C[i][j] = C[i-1][j]+C[i-1][j-1], j++);
    for(rint i = fac[0] = 1; i <= 15; fac[i] = 1ll*fac[i-1]*i, i++);
    n = rf(); K = rf(); printf("pi = %.14Lf\n",(db)PI*(db)PI/6);
    for(rint i = 1; i <= n+K; A[i] = A[i-1]+(db)1/(1ll*i*i), i++);
    printf("         "); for(rint j = 0; j <= K; printf("Richardson %2d:    ",j), j++); puts("");
    for(rint i = 1, j; i <= n; i++) for(printf("n = %3d: ",i), j = 0; j <= K; printf("%.14Lf %c",Richardson(j,i),"\n "[j<K]), j++);
    return 0;
}

下面是实测结果:

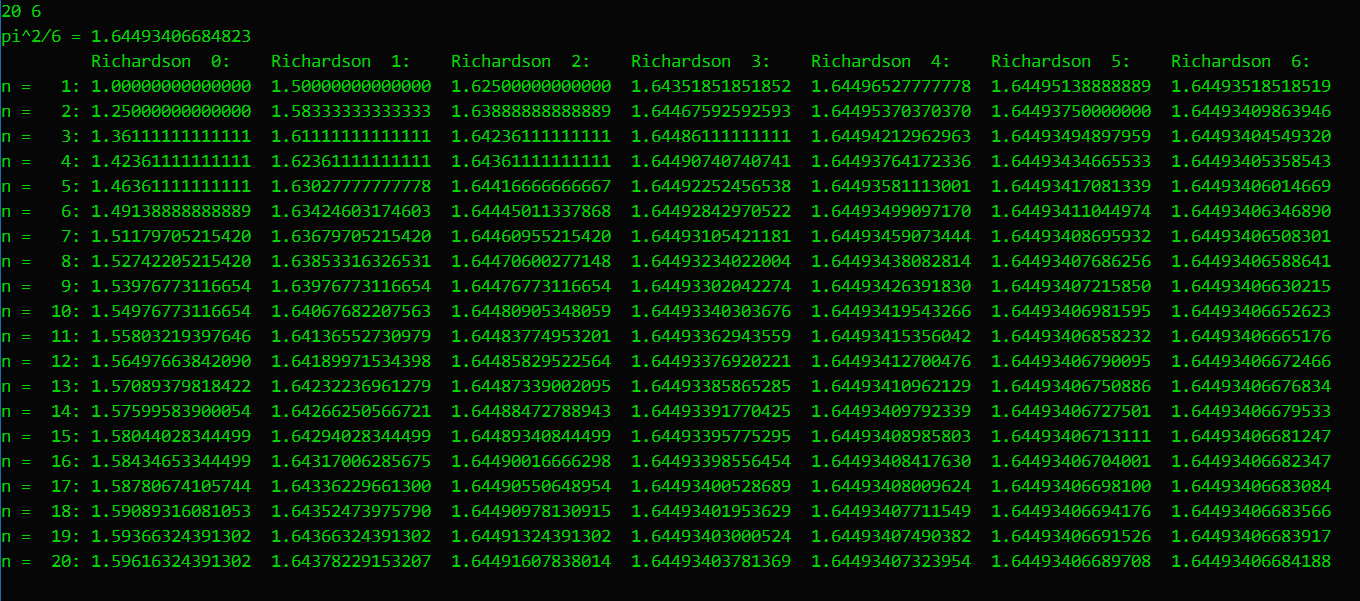
可以看到高阶Richardson出奇的有效，10位小数的精度都已经不足以体现出区别。

当然，在高阶Richardson的基础上在进行层层嵌套，应该可以得到更优秀的结果……

总结

Shanks变换和Richardson外推法都是通过构造一个带有附加项的近似序列来解决收敛级数求和的问题。

Shanks变换更适用于交错数列，Richardson外推法更适用于单调数列。

注意两者都只用到了数列的某几项的信息。这意味着这两种方法不依赖于具体的数列/函数。同样这也意味着两种方法存在不足: 无法预测存在"突变"的函数。

扫描二维码即可在手机上查看这篇文章，或者转发二维码来分享这篇文章: