继续留遗产…
UPD2019.06.15: PDF版本链接
网页较大预警。如果公式解析不正确请刷新页面。长时间加载不出来建议打开PDF用Ctrl+S键下载到本地。流量访问请谨慎。
高考完继续留遗产…
整理了一下笔记,
也许是面向后来要补文化课的竞赛选手的。本来想高考前发出来的,结果本地Markdown语法和博客的Markdown语法解析不兼容,高考前不想浪费时间,现在花了较长时间调整可以放出来了。也是由于语法解析不兼容的缘故,已经尽可能修正了,最后Markdown排版还是有点小问题~~,凑合看吧~~。而且公式比较多,网页解析可能比较慢,稍等一会儿即可。
虽然自己挺菜的,不过感觉整理的比较全面,除了一些特别简单和特别超纲的知识点就没有涉及,可能存在少部分超纲内容,仅供参考(面向对象也许是全国I卷570 ~ 640吧,这个说不好~~,主要是高考之前也不敢乱说~~)。
免责声明:文章中存在错误是难免的~~,后果自负~~,欢迎大佬联系指正或默默走开。且据目前统计来看有较大概率出现错别字。数学选修极坐标单独整理了,不等式整理较少,主要在基本运算部分。
对于数学学科来说,公式应该总结的非常全面了,不过数学题更多的还是大量题目训练、计算能力
和智商,仅仅掌握基础知识和公式是不够的。笔记中的一些运算技巧起码个人感觉可以说是非常有用了。也许有较多超纲内容?建议以题目训练为主,这里的笔记仅仅是提醒、提供一些技巧。高考加油!!!
UPD2019.06.24: 高考667分。所以面向对象也许是570 ~ 667(雾)。
基本运算
-
立方差公式
-
二次方程韦达定理
方程有两个正根 。
方程有两个负根 。
方程有两个异号根 。
方程有两个根均大于 。
方程有两个根均小于 。
方程有两个根在两侧 。
方程有两个根在之间 。
方程有两个根在之间 。
方程有两个根,一个在之间 。
方程有两个根,一个在之间 。
-
高次不等式: 穿根法,因式分解数轴标根,二次因式不穿过数轴。分式不等式可以分子分母分解因式后视作相乘,穿根后注意抠点。
-
绝对值不等式: 。
-
均值不等式链: 当时:
对数平均值结论不直接用于导数题的证明,但是证明对数平均值的方法可以作为证明导数题的思路。对数平均值的位置可以构造后转化为的函数求导加以证明,如证明对数平均大于几何平均: 。
推论:
$$
\underbrace{ab}_{几何} \le \underbrace{\frac{(a+b)^2}{4}}_{算术} \le \underbrace{\frac{a^2+b^2}{2}}_{平方} \\
\underbrace{2\sqrt{ab}}_{几何} \le \underbrace{a+b}_{算术} \le \underbrace{\sqrt{2(a^2+b^2)}}_{平方} \\
\underbrace{2\sqrt{AB}}_{几何} \le \underbrace{At + B\frac{1}{t}}_{算术} \\
$$
-
积和并存式的化简(如)
- 换元法: ,,即可解二次不等式求出的范围,进而求出最小值以及最小值。
- 乘一法: 当时有,同除得,则可求,然后化简套用均值不等式即可。
- 配方法: 如,然后对和套用均值不等式即可。
-
三角不等式
-
柯西不等式
-
常用不等式: 。
-
等差数列快速求和及差分:
-
等比数列快速求和:
令就得到:
求和上下界差分就得到:
这一结论常可以被用于裂项相消过程中快速求出项的通式。具体计算裂项相消化简就得到:
这个式子看上去没有规律,深入理解其物理意义: 因为有,代入整理再代入第二个式子就得到:
所以第三个式子的本质就是横向求和和纵向求和的转化,这样就方便记忆和使用了。
集合
-
集合满足确定性、互异性、无序性。
-
空集是任何集合的子集,是任何非空集合的真子集。
-
个元素()有个子集,个真子集,个非空子集,个非空真子集。空集只有一个子集,没有真子集、非空子集、非空真子集。
-
德摩根律: ,。
-
映射: ,两个非空集合和之间存在着对应关系,且中任何一个元素(原象)有一个唯一、确定的中元素(象)与其对应,记做。为定义域,所有构成的集合为值域(不一定为)。
一个映射如果则称为满射(中每个元素都被对应到),如果则称为单射(中每个元素对应不同元素),既是满射又是单射的映射为双射/一一映射。
,共有种;其中单射有种;满射个数只能递推或求和求出,没有一个单项通项。
,双射共有种。
如果为非空数集,那么称一个映射为函数。
-
集合的表示:
列举法:
描述法:
符号法: 非负整数集(自然数集);正整数集(其他正集同理,如);整数集;有理数集;实数集;复数集。
数集的区间表示。
图示法: Venn图。
函数
-
单调性: 。或。
复合函数单调性: 同增异减。
函数单调性的推论: 对于一个在一段区间内的连续函数,。
-
奇偶性: 定义域对称且为偶函数,定义域对称且为奇函数。只有既奇又偶。
复合函数奇偶性: 同奇才奇。奇偶性: 同偶异奇。
任何一个函数都可以拆分为一个奇函数与一个偶函数之和:
奇函数关于原点对称,偶函数关于轴对称。
-
函数的零点: 则称为函数的一个零点(是一个数而不是一个点)。
则区间内存在奇数个变号零点。
-
正比例函数:
幂型函数:
对数型函数:
指数型函数:
-
对数函数性质
-
反函数性质
-
将函数表达式中的与互换,定义域和值域互换。
-
反函数图像与原图像关于对称,对应位置切线斜率互为倒数,若原函数过点,则反函数过点。
-
反函数对应区间单调性与原函数相同。
-
非一一映射的函数没有反函数。
-
-
定义域问题:
- 分数函数 分母不为0
- 根号函数 根号下大于等于0
- 对数函数 底数大于0且不为1,真数大于0
- 指数函数 无意义
-
周期问题
- ,则的一个周期为。
- ,则的一个对称轴为。
- 有两条对称轴,则的一个周期为。
- 有两个对称中心,则的一个周期为。
- 有对称轴,对称中心,则的一个周期为。
三角函数
-
任意角的大小比较: 按照弧度制实数比较,。
锐角、直角与钝角定义不变。
和一个角共终边的所有角: 。
-
方位角: 从正北方向顺时针旋转的角度。
坡度: 坡面与水平面所成二面角的正切值。
-
弧度制
,。
弧长与扇形面积:
-
任意角三角函数,对于点,距离原点距离,圆心角。
\begin{align} 正弦\sin \theta = \frac{y}{\rho}\;\;\;\; & 余割 \csc \theta = \frac{\rho}{y} = \frac{1}{\sin \theta} \\ 余弦\cos \theta = \frac{x}{\rho}\;\;\;\; & 正割 \sec \theta = \frac{\rho}{x} = \frac{1}{\cos \theta} \\ 正切\tan \theta = \frac{y}{x}\;\;\;\; & 余切 \cot \theta = \frac{x}{y} = \frac{1}{\tan \theta} \\ \end{align} -
三角函数公式
\begin{align} & \tan \alpha = \frac{\sin \alpha}{\cos \alpha} \\ & \sin^2 \alpha + \cos^2 \alpha = 1 \\ & \csc^2 \alpha - \cot^2 \alpha = \frac{1}{\sin^2 \alpha} - \frac{1}{\tan^2 \alpha} = 1 \\ & \sec^2 \alpha - \tan^2 \alpha = \frac{1}{\cos^2 \alpha} - \frac{1}{\tan^2 \alpha} = 1 \\ & \cos(\alpha \pm \beta) = \cos \alpha \cos \beta \mp \sin \alpha \sin \beta \\ & \sin(\alpha \pm \beta) = \sin \alpha \cos \beta \pm \cos \alpha \sin \beta \\ & \tan(\alpha \pm \beta) = \frac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta} \;\;\;\;(注意定义域)\\ & \sin 2\alpha = 2\sin \alpha \cos \alpha \\ & \cos 2\alpha = 2\cos^2 \alpha - 1 = 1 - 2\sin^2 \alpha = cos^2 \alpha - sin^2 \alpha = (\cos \alpha + \sin \alpha)(\cos \alpha - \sin \alpha) \\ & \tan 2\alpha = \frac{2\tan \alpha}{1 - \tan^2 \alpha} \\ & \cos^2 \alpha = \frac{1 + \cos 2\alpha}{2} \\ & \sin^2 \alpha = \frac{1 - \cos 2\alpha}{2} \\ & (\sin \alpha \pm \cos \alpha)^2 = 1 \pm \sin 2\alpha \\ \end{align}万能替换公式: 。
辅角公式:
和差化积与积化和差:(以为例)
\begin{align} & \cos(\alpha + \beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta\;\;\;\;①\\ & \cos(\alpha - \beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta\;\;\;\;②\\ & \frac{①+②}{2} \Rightarrow \cos \alpha \cos \beta = \frac{1}{2}[\cos(\alpha + \beta)+\cos(\alpha - \beta)]\;\;\;\;(积化和差) \\ & 用A,B代\alpha + \beta,\alpha - \beta \Rightarrow \cos(\frac{A+B}{2}) \cos(\frac{A-B}{2}) = \frac{1}{2}(\cos A + \cos B)\;\;\;\;(和差化积) \\ \end{align}UPD2019.11.05: 和差化积利用复数证明:
三角函数求值常用变换
-
同乘、除,或将原式中的1与其互换。经常通过平方配成齐次式。
-
分子分母同时乘、除、或,并利用。
-
,,相互转化。
诱导公式:
- 整圈不变: ,。
- 半圈相反: ,。
- 加直求导: ,。
- 减直积分: ,。
- 正奇余偶: ,。
- 正余互余: ,。,。
- 切直负变: ,。
-
-
三角函数线: 有向线段
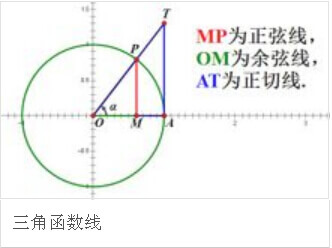
-
三角函数图像
左加右减,上加下减,所有操作针对自变量。
正弦型函数: 。频率;最小正周期;振幅;相位;初相。
五点法: 。
正切型函数: 注意定义域。最小正周期。
-
三角形中的三角函数
-
三角形中角度关系
-
正弦定理
推论:
-
余弦定理
推论:
-
海伦公式
记,则有
-
-
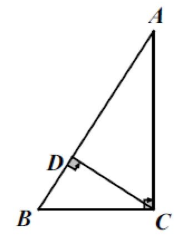
射影定理
向量
-
相等向量: 共基线,方向相同且模长相等
相反向量: 共基线,方向相反且模长相等
同向向量: 共基线,方向相同
反向向量: 共基线,方向相反
等长向量: 模长相等
向量垂直: 基线垂直。
平行向量/共线向量: 基线平行或重合。
垂直、平行于任何向量,但其与另一个向量的夹角只能是0或而不能是其他角度。
-
(矩形对角线相等)
(直角三角形斜边中线)
-
判断向量共线/三点共线:
-
或存在使得 向量共线。
-
对于平面内任意一点和线段上一点,存在唯一一组,使得且:
其中有(即加权重心)。
-
-
-
平面向量基本定理: 选择平面内任意不共线向量。向量。
单位正交基底: 。
-
向量点积: 。其中称为在上的投影。
推论:
-
向量与平面几何()
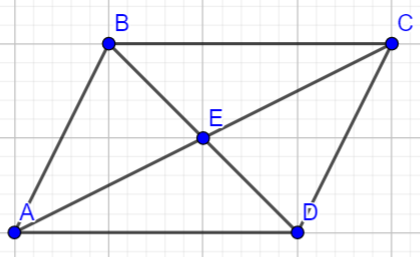
平行四边形四边对角线平方和定理:
()
极化恒等式:
()
斯图尔特公式,对于上任意一点都有存在唯一一组,使得且:
其中有(即加权重心)。
(,代入余弦定理)。
-
向量旋转公式
-
空间向量: 与平面向量几乎完全相同。
记,,。
平面三角形面积:
空间四面体体积:
空间三角形面积:
注意这里是向量模长而非绝对值,也可用海伦公式计算。
逻辑、统计与概率
-
命题的等价形式
原命题 逆否命题;逆命题 否命题;注意否命题与命题的否定不同。
-
(第一)数学归纳法
要证明: 对于任意,为真。
(1) 当时,为真。
(2) 假设当时为真(),当时(即)也为真。直接从出发运用分析法,最后得到。
(3) 由(1),(2)则对于任意,为真。
-
频率分布直方图(纵轴为频率/组距,所有柱形面积和为1)
平均数: 每个柱形视作中值,求平均。
中位数: 面积恰好1/2处的值。
众数: 取最高的柱形中值。(注意平均数和中位数只有一个,众数可以有多个)。
-
回归分析
检验数据的相关性(只有相关性高才有求回归直线的价值):
恒成立,当趋近于1时正相关性很高,当趋近于时负相关性很高,当趋近于0时相关性较弱。
求满足最小化,称为这组数据的回归直线。有:
对于一类的函数常两边取对数后用回归曲线拟合: 。
-
独立性检验
越大,两者相关性越强。注意分子为5次式,而分母为4次式,这意味着样本数目数量级越大时得出的两者相关性强的结论往往更可靠,这与常识相吻合。
-
二项式展开式
即次数较大的项在前。
-
分布
-
两点分布:
-
二项分布:
-
超几何分布:
-
正态分布:
-
标准正态分布:
-
立体几何
-
投影
直观图(斜二测画法): 长度不变,长度变成原来,沿方向。平面上的图形,直观图面积是原图形面积的。
-
简单几何体
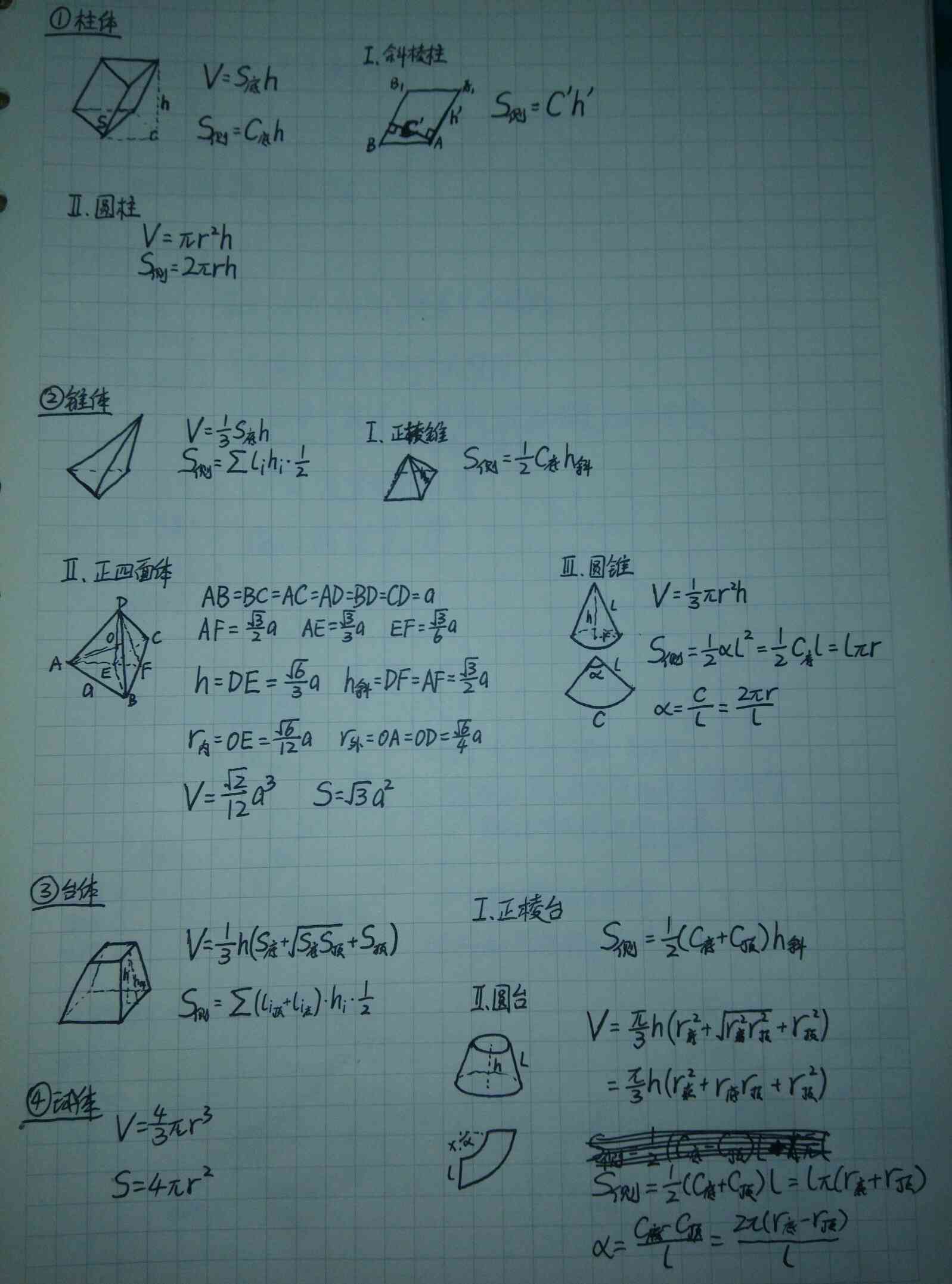
-
三视图: 直接构造法、补形法(交线法、删点法)。
-
空间几何证明
-
公理
公理1: 如果一条直线上的两点在一个平面内,那么这条直线上的所有点都在这个平面内。。
公理2: 如果两个不重合的平面有一个公共点,那么它们有且仅有一条经过该点的公共直线 。
公理3: 经过不在一条直线上的三点,有且只有一个平面。。
推论1: 经过一条直线和这条直线外一点,有且仅有一个平面。
推论2: 经过两条相交直线,有且仅有一个平面。
推论3: 经过两条平行线,有且仅有一个平面。
平行公理:平行于同一直线的两条直线互相平行。。
等角定理:如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补。
-
线面平行判定定理: 平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。。
线面平行性质: 一条直线和一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。。
-
面面平行判定定理: 如果一个平面内有两条相交直线与另一个平面平行,那么这两个平面平行。。
推论: 如果一个平面内有两条相交直线分别与另一个平面内的两条相交直线平行,那么这两个平面平行。。
面面平行传递性: 平行于同一平面的两个平面互相平行。。
面面平行性质: 两个平面平行,在一个平面内的任意一条直线平行于另外一个平面。。
-
线面垂直判定定理: 如果一条直线与平面内两条相交直线都垂直,那么这条直线与这个平面垂直。。
线面垂直性质: 如果一条直线垂直于一个平面,那么该直线垂直于平面内的所有直线。。
-
面面垂直判定定理: 一个平面过另一平面的垂线,则这两个平面相互垂直。。
面面垂直性质: 如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。。
-
-
空间角
订正: 异面直线所成角一般被称为线线角,范围是而不是。感谢@xizeyoupan提醒。

-
外接圆和外接球
- 直接构造: 利用中垂线相交求出圆心、球心。
- 补形法。
- 正弦定理。
- 正四面体。
内接圆和内接球
- 直接构造: 利用角平分线相交求出圆心、球心。
- 等面积/体积法: ,。
- 正四面体。
- 内心性质: 的三边为,内心。
解析几何
-
直线解析式
点斜式:
斜截式:
两点式:
一般式:
截距式:
-
直线一般式
-
;;。直线的一个法向量。
-
直线平行或重合: 。注意如果只考虑平行时要排除重合情况。
直线垂直: 。
-
点到直线距离: 有向距离,其中以的方向为正方向。
平行直线间的距离: 。
平行直线间的铅垂高差: 。
-
关于点的对称变换:
-
关于直线的对称点:
-
过两条直线交点的直线系:
-
-
线性规划
-
转为直线切凸包。
-
转为到原点距离。
-
转为过一点斜率。
-
其余情况先变换为以上三种或其他几何意义。
-
-
圆
-
标准方程:
一般方程:
其中,,。
-
圆的位置情况:
相离 有4条公切线
外切 有3条公切线
相交 有2条公切线
内切 有1条公切线
内含 有0条公切线
当两圆外切时两圆方程作差即可得到垂直于圆心连线的公切线方程;相交时两圆方程作差即可得到相交弦方程;内切时两圆方程作差即可得到公切线方程。
-
切点弦方程
对于任意圆和圆锥曲线上一点,用代,用代,用代,用代就得到过点的切线方程。
对于圆来说,如果点不在圆上而在圆外,那么得到切点弦方程。如果在圆内同样得到一条直线方程,满足。
-
直径圆方程
以和为直径的圆: 。本质是圆周上点到直径端点连线垂直,对应向量点积为0。
-
-
圆锥曲线
-
椭圆: 平面内与两点距离和为定值的曲线()。
方程: 或()。
离心率: ,离心率越大椭圆越扁。
特殊点: 或在椭圆上。
通径: ,同时为过椭圆焦点的最短弦长。
焦点三角形: 椭圆上任意一点,有,其中:
焦半径: 椭圆上任意一点, ,。
-
双曲线
方程: 或()。
离心率: ,离心率越大双曲线开口越大。
特殊点: 或在双曲线上。
通径: ,同时为过双曲线焦点的最短弦长。
渐近线: 或(即)。
焦点三角形: 双曲线上任意一点,有,其中:
-
抛物线
方程: 或()。
离心率: 。
准线: 或。
特殊点: 或在抛物线上;或在抛物线上。
通径: ,同时为过抛物线焦点的最短弦长。
切线性质: 以为例: ,抛物线过的切线切点为。
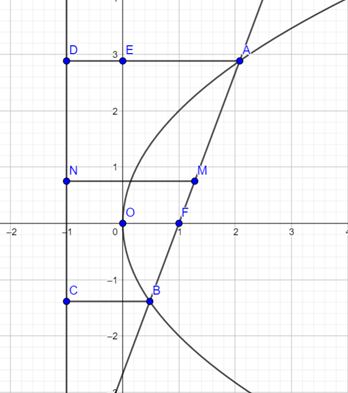
圆切性质: 以为例:
以AB为直径的圆与CD相切于点N,且AN,BN与抛物线相切。
以CD为直径的圆与AB相切于点F。 。
以AF为直径的圆相切于轴。(对BF也成立)
以OE为直径的圆相切于AF。(对BF也成立)
焦半径: 以为例: 记直线倾斜角为,
-
圆锥曲线
第二定义: 。当时为椭圆, 时为双曲线,时为直线。
椭圆和双曲线焦点三角形涉及面积问题的几何法,设:
-
-
解析几何常用结论
-
角平分线性质
对于角平分线平行于或轴时,。
内/外角平分线定理(角的内/外角平分线交所在直线于,都有)。
角平分线上对称两点到角平分线距离相等(定义,不常用)。
-
圆定义
到一个点距离为定值的所有点。
对两个点,满足的所有点。
对两个点,的所有点。
对,且为凸四边形的所有点。
-
相交弦定理
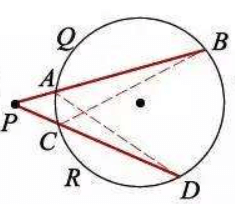
恒成立(包括点在圆内的情况)
-
快速联立运算
对于形似的条件往往直接通分运算,而当左右倍数相同,如则直接提取公因式,如:
-
垂直的转化
- 转化为圆周上的点根据圆的性质计算
-
对称构造
对于椭圆外一点作一条椭圆的线,讨论时,构造关于的对称式:
然后再由对勾函数的单调性求出的范围条件。
对于不对称的多条直线问题,如和交于一点,往往可以交换两条直线要求和同时交于一点,然后利用这四条直线即可构造对称式。
一些非对称式可以直接代入韦达定理,如。最后的理想结果是分子分母同时含有带有的等比项,直接约分消去。
-
抛物线
当直线与抛物线联立的时候,求值代入时更多用而非椭圆和圆锥曲线时用进行和的转化,这个技巧往往对运算量有巨大影响!
-
导数与积分
-
导数:
在数形结合方面常有。
奇函数的导数是偶函数,偶函数的导数是奇函数。
较少用公式: ;。
-
切线方程:
在点处的切线: 。
过点处的切线,设切点: ,就可以解出,进而求出切线。
-
极值点: 函数在该点左右两侧邻近位置值都大/小于该点。区间端点不是极值点。同零点,极值点是一个横坐标。
最值点 = 所有极值点和区间端点中函数最大/小值点。
-
双变量偏移问题: 对称和问题


-
积分: 记,则
较少用公式: 。
求积分:
-
利用奇偶性求积分: 当关于原点对称时奇函数积分为0。
-
利用几何法求积分
如几何意义为所有到原点距离为3的点的纵坐标之和,即的半圆面积。
-
原函数的构造
- 麦克劳林级数
常见函数:
极坐标与参数方程
-
。
-
。(正弦定理推论)。
-
过原点的圆的极坐标通式: ,表示以轴为起始逆时针旋转弧度得到的圆(顺加逆减)。
-
直线的参数方程: 。直线过点,倾斜角,斜率。
的几何意义是到的有向距离,注意判断的符号。
对于非标准的直线参数方程使用的几何意义时一定要保证。
-
椭圆的参数方程: 。注意对于椭圆上一点,并不是。
扫描二维码即可在手机上查看这篇文章,或者转发二维码来分享这篇文章:

